We will now define the notion of a random variable.
Very loosely speaking, a random variable is a numerical quantity that takes random values.
But what does this mean? We want to be a little more precise and I’m going to introduce the idea through an example.
Suppose that our sample space is a set of students labeled according to their names.
Or for simplicity, let’s just label them as a, b, c, and d.
Our probabilistic experiment is to pick a student at random according to some probability law and then record their weight in kilograms.
So for example, suppose that the outcome of the experiment was this particular student, and the weight of that student is 62.
Or it could be that the outcome of the experiment is this particular student, and that particular student has a weight of 75 kilograms.
The weight of a particular student is a number, little w.
But let us think of the abstract concept of weight, something that we will denote by capital W.
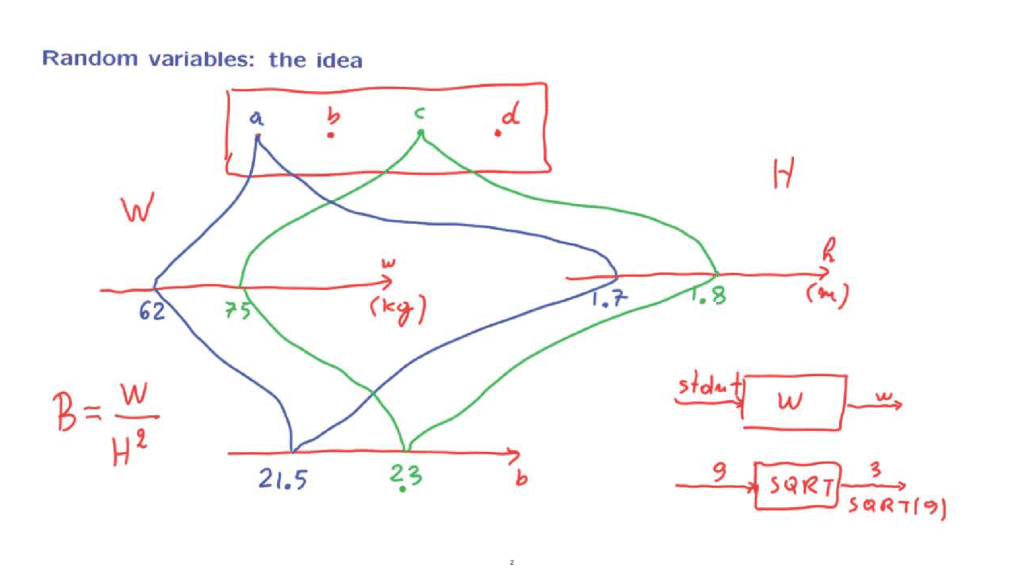
Weight is an object whose value is determined once you tell me the outcome of the experiment, once you tell me which student was picked.
In this sense, weight is really a function of the outcome of the experiment.
So think of weight as an abstract box that takes as input a student and produces a number, little w, which is the weight of that particular student.
Or more concretely, think of weight with a capital W as a procedure that takes a student, puts him or her on a scale, and reports the result.
In this sense, weight is an object of the same kind as the square root function that’s sitting inside your computer.
The square root function is a function.
It’s a subroutine, perhaps it is a piece of code, that takes as input a number, let’s say the number 9, and produces another number.
In this case, it would be the number 3, which is the square root of 9.

Notice here the distinction that we will keep emphasizing over and over.
Square root of 9 is a number.
It is the number 3.
The box square root is a function.
Now, let us go back to our probabilistic experiment.
Note that a probabilistic experiment such as the one in our example can have several associated random variables.
For example, we could have another random variable denoted by capital H, which is the height of a student recorded in meters.
So if the outcome of the experiment, for example, was student a, then this random variable would take a value which is the height of that student, let’s say it was 1.7.
Or if the outcome of the experiment was student c, then we would record the height of that student.
And let’s say it turns out to be 1.8.
Once again, height with a capital H is an abstract object, a function whose value is determined once you tell me the outcome of the experiment.
Now, given some random variables, we can create new random variables as functions of the original random variables.
For example, consider the quantity defined as weight divided by height squared.
This quantity is the so-called body mass index, and it is also a function on the sample space.
Why is it a function on the sample space? Well, because once an outcome of the experiment is determined, suppose that the outcome of the experiment was the blue student, then these two numbers, 62 and 1.7, are also determined.
And using those numbers, we can carry out this calculation and find the body mass index of that particular student, which in this case would be 21.5.
Or if it happened that this student was selected, then the body mass index would turn out to be some other number.
In this case, it would be 23.
So again, we see that the body mass index can be viewed as an abstract concept defined by this formula.
But once an outcome is determined, then the body mass index is also determined.
And so the body mass index is really a function of which particular outcome was selected.

Let us now abstract from the previous discussion.
We have seen that random variables are abstract objects that associate a specific value, a particular number, to any particular outcome of a probabilistic experiment.
So in that sense, random variables are functions from the sample space to the real numbers.
They are numerical functions, but as numerical functions they can either take discrete values, for example the integers, or they can take continuous values, let’s say on the real line.
For example, if your random variable is the number of heads in 10 consecutive coin tosses, this is a discrete random variable that takes values in the set from 0 to 10.
If your random variable is a measurement of the time at which something happened, and if your timer has infinite accuracy, then the timer reports a real number and we would have a continuous random variable.
In this lecture sequence and in the next few ones, we will concentrate on discrete random variables because they are easier to handle.
And then later on, we will move to a discussion of continuous random variables.
Throughout, we want to keep noting this very important distinction that I already brought in the discussion for a particular example, but it needs to be emphasized and re-emphasized.
That we make a distinction between random variables, which are abstract objects.
They are functions on the sample space and they are denoted by uppercase letters.
In contrast, we will use lower case letters to indicate numerical values of the random variables.

So little x is always a real number, as opposed to the random variable, which is a function.
One point that we made earlier is that for the same probabilistic experiment we can have several random variables associated with that experiment.
And we can also combine random variables to form new random variables.
In general, a function of random variables has numerical values that are determined by the numerical values of the original random variables.
And so, ultimately, they are determined by the outcome of the experiment.
So a function of random variables has a numerical value which is completely determined by the outcome of the experiment.
And so a function of random variables is also a random variable.
As an example, we could think of two random variables, X and Y, associated with the same probabilistic experiment.
And then define a random variable, let’s say X plus Y.
What does that mean? X plus Y is a random variable that takes the value little x plus little y when the random variable capital X takes the value little x and capital Y takes the value little y.
So X and Y are random variables.
X plus Y is another random variable.
X and Y will take numerical values once the outcome of the experiment has been obtained.
And if the numerical values that they take are little x and little y, then the random variable X plus Y will take the numerical value little x plus little y.
So we can now move on and start doing some interesting things about random variables.
Characterize them, describe them, give some examples, and introduce some new concepts associated with them.