Besides PMFs and PDFs, we can also describe the distribution of a random variable, as we know, using a CDF.
A CDF is always well-defined.
And for the case of a continuous random variable, the CDF can be found by integrating the PDF.
And conversely, we can recover the PDF from the CDF by differentiating.
There is something similar that happens for the case of multiple random variables, as well.
We can define the joint CDF as the probability that X and Y, the pair X-Y, takes values that are below certain numbers, little x and little y.
So we are talking about the probability of the blue set in this diagram.
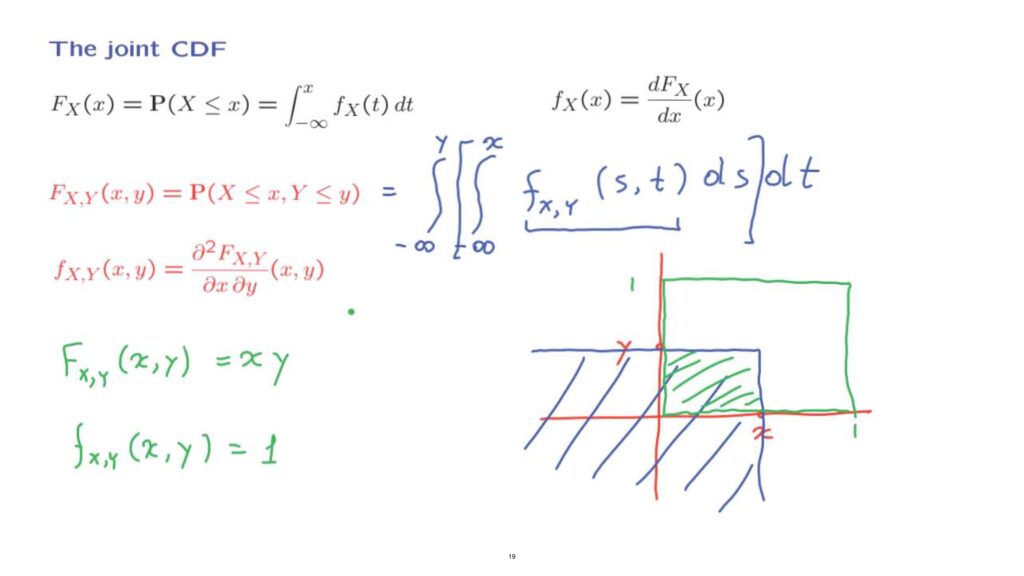
This probability can be found by integrating the joint PDF over the blue set.
And, since we’re using x and y to be some specific numbers, let us use some different dummy variables to carry out the integration.
What is the range of the integration? The first variable, which is s in this integral, ranges from minus infinity up to x.
And the other variable, which is the one that we’re integrating with respect to, in the outer integral– the t variable– ranges from minus infinity to y.
Now, let us see what happens if we start taking derivatives of this expression.
If we take the derivative of this expression with respect to y, what is left is the inner integral.
And if we take, now, a derivative with respect to x of this inner integral, we will be left with just the joint PDF.
And it will be the joint PDF evaluated at the particular limits of the integration.
So, it’s going to be f sub xy at little x, little y.
So, we have this particular formula.
By taking derivative with respect to x, and then with respect to y, or maybe in the opposite order.
It doesn’t matter.
This particular derivative gives us back the PDF.
Let us look at an example.
Suppose that we have a uniform distribution on the unit square.

So the PDF is equal to 1 on this green square.
And is equal to 0 otherwise.
So, in this example, if we take some x and y, so that the xy pair falls inside the rectangle, the probability of the blue set is going to be just the probability of that little rectangle here.
Because everything outside has zero probability.
With a uniform joint PDF, which is equal to 1, the probability is just the area of the set that we are considering.
And since this set that we are considering is a rectangle with [sides] x and y, the joint CDF is equal to x times y.
Now, if we take the derivative of this expression with respect to x, and then with respect to y, then we’re left just with a constant equal to 1– which is as it should be, so that it integrates to one.
So, we have seen that CDFs also apply to the case of multiple random variables, and that we can recover the joint PDF from the joint CDF.