We now move to a new topic– conditioning.
Every probabilistic concept or probabilistic fact has a conditional counterpart.
As we have seen before, we can start with a probabilistic model and some initial probabilities.
But then if we are told that the certain event has occurred, we can revise our model and consider conditional probabilities that take into account the available information.
But as a consequence, the probabilities associated with any given random variable will also have to be revised.
So a PMF will have to be changed to a conditional PMF.
Let us see what is involved.
Consider a random variable X with some given PMF, whose values, of course, sum to 1, as must be true for any valid PMF.

We are then told that a certain event, A, has occurred.
In that case, the event that X is equal to– little x– will now have a conditional probability of this form.
We will use this notation here to denote the conditional probability that the random variable takes the value little x.
Notice that the subscripts are used to indicate what we’re talking about.
In this case, we are talking about the random variable X in a model where event A is known to have occurred.
Of course, for this conditional probability to be well defined, we will have to assume that the probability of A is positive.
This conditional PMF is like an ordinary PMF, except that it applies to a new or revised conditional model.

As such, its entries must also sum to 1.
Now the random variable X has a certain mean, expected value, which is defined the usual way.
In the conditional model, the random variable X will also have a mean.
It is called the conditional mean or the conditional expectation.
And it is defined the same way as in the original case, except that now the calculation involves the conditional probabilities, or the conditional PMF.
Finally, as we discussed some time ago, a conditional probability model is just another probability model, except that it applies to a new situation.
So any fact about probability models– any theorem that we derive– must remain true in the conditional model as well.
As an example, the expected value rule will have to remain true in the conditional model, except that, of course, in the conditional model, we will have to use the conditional probabilities instead of the original probabilities.
So to summarize, conditional models and conditional PMFs are just like ordinary models and ordinary PMFs, except that probabilities are replaced throughout by conditional probabilities.
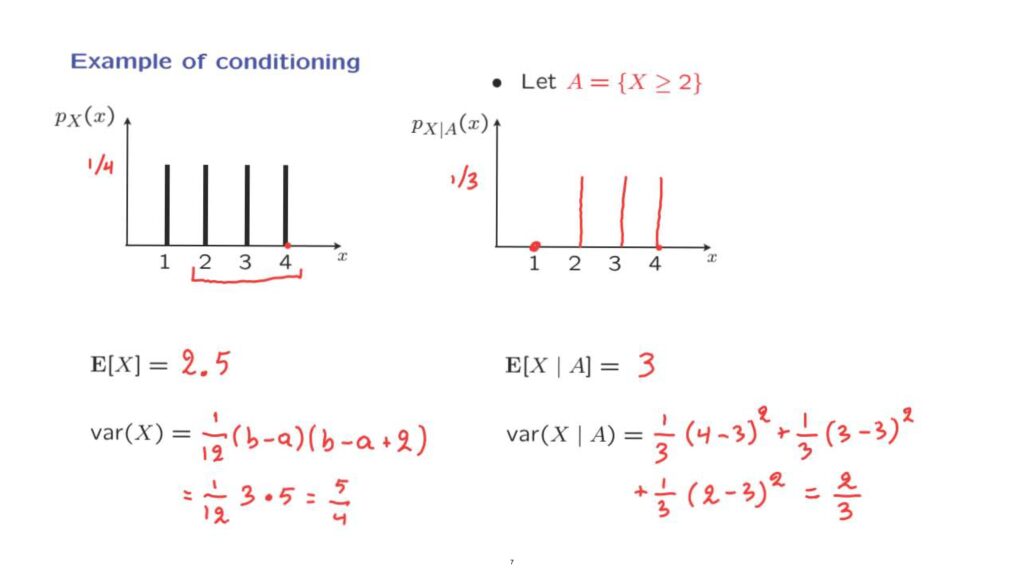
Let us now look at an example.
Consider a random variable, which in this case, is uniform, takes values from 1 up to 4.
So each one of the possible values has probability 1 over 4.
For this random variable, we can calculate the expected value, which by symmetry is going to be the midpoint.
So it is equal to 2 and 1/2.
We can also calculate the variance.
And here we can apply the formula that we have derived earlier– 1/2 times b minus a times b minus a plus 2.
And in this case, it’s 1 over 12 times b minus a is 4 minus 1, which is 3.
And the next term is 5.
And after we simplify, this is 5 over 4.
Suppose that now somebody tells us that event A has occurred, where event A is that the random variable X takes values in the range 2, 3, 4.

What happens now? What is the conditional PMF? In the conditional model, we are told that the value of 1 did not occur, so this probability is going to be 0.
The other three values are still possible.
What are their conditional probabilities? Well, these three values had equal probabilities in the original model, so they should have equal probabilities in the conditional model as well.
And in order for probabilities to sum to 1, of course, these probabilities will have to be 1/3.
So this is the conditional PMF of our random variable, given this new or additional information about the outcome.
The expected value of the random variable X in the conditional universe– that is, the conditional expectation– is just the ordinary expectation but applied to the conditional model.
In this conditional model, by symmetry, the expected value will have to be 3, the midpoint of the distribution.
And we can also calculate the conditional variance.
This is a notation that we have not yet defined, but at this point, it should be self-explanatory.

It is just the variance of X but calculated in the conditional model using conditional probabilities.
We can calculate this variance using once more the formula for the variance of a uniform distribution, but we can also do it directly.
So the variance is the expected value of the squared distance from the mean.
So with probability 1/3, our random variable will take a value of 4, which is one unit apart from the mean, or more explicitly, we have this term.
With probability 1/3, our random variable takes a value of 3.
And with probability 1/3, our random variable takes the value of 2.
This term is 0.
This is 1 times 1/3.
From here we get another 1 times 1/3.
So adding up, we obtain that the variance is 2/3.
Notice that the variance in the conditional model is smaller than the variance that we had in the original model.
And this makes sense.
In the conditional model, there is less uncertainty than there used to be in the original model.
And this translates into a reduction in the variance.
To conclude, there is nothing really different when we deal with conditional PMFs, conditional expectations, and conditional variances.
They are just like the ordinary PMFs, expectations, and variances, except that we have to use the conditional probabilities throughout instead of the original probabilities.