Before we dive into the heart of the subject, I want to make a few comments on the different problem types that show up in the field of inference.
You can think of a general distinction between model building versus making inferences about unobserved variables.
We said a little earlier that one of the main uses of the field of inference is to construct models of certain situations.
But in many cases, we already have a model.
On the other hand, there may be variables that are unknown, that are unobserved– variables that are part of the model, but whose values are not known.
In such cases, we still want to use data to make some predictions or decisions about those unobserved variables.
So model building might or might not be part of the problem that we’re dealing with.
To illustrate the difference between these two versions of the problem, let us think of a concrete setting.
You have a transmitter who is sending a signal.
Call it S.
And that signal goes through some medium.
It could be just the atmosphere.
And what that medium does is that it attenuates the signal by a certain factor, a.
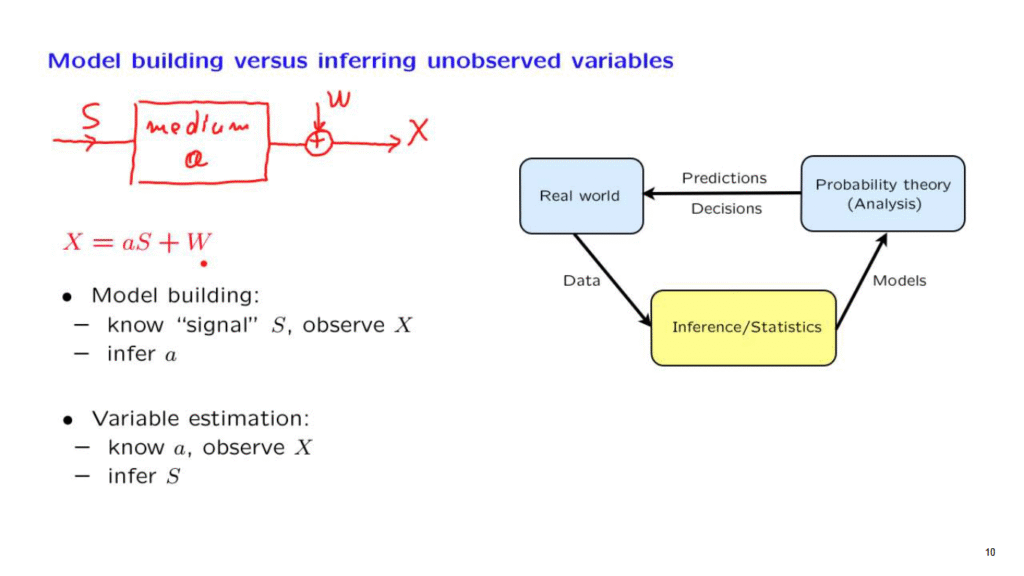
And then as the signal travels, it also gets hit by some noise, call it W, and what the receiver sees is an observation, X.
So the situation is described by this simple equation here.
This situation often brings up the following inference problem.
We want to find out what the medium is.
How do we do this?
We send a pilot signal, S, that is a signal that we know what it is.
We observe X, and then using this equation, and, knowing that W is random noise coming from some distribution, we try to make an inference about the variable a.
So this is an instance of model building.
We’re trying to make a model of the medium that’s involved.
But we can also think of a different problem.
Suppose that we know what the medium is.
Perhaps we already went through this particular phase here.
But we’re sitting at the receiver, and we do not know what has been sent.
And we want to find out what S is.
So we are looking again at this equation.
This time we know a, and we’re trying to make inferences about S.
You notice that these two versions of the problem are essentially of the same mathematical structure.
We have a linear equation.
In one case, we know S.
We want to find out a.

In the other case, we know a.
We want to find out what S is.
So even though the interpretation of these two problems [is] quite different, the mathematical structure is exactly the same.
This is fortunate.
It means that one and the same methodology would be applicable to both types of problems.
There is another distinction between problem types which turns out to be a little more substantial.
There are problems that we call hypothesis testing problems.
In those problems the unknown takes one out of a few possible values.
That is, we may have a few different alternative models of the world.
And we’re trying to figure out which one of those models is the correct one.
We’re going to decide in favor of one of the candidate models, and what we want to achieve is that we make a correct decision.
Or if not, we want to have a small probability of making an incorrect decision.
An example of this kind is the radar detection problem that we had discussed in the very beginning of this course, in which we were getting a signal.
We were getting a radar reading.
And the question was to make an inference whether the radar is seeing an airplane or whether an airplane is not present.

So in hypothesis testing problems, we’re essentially making a choice out of a small number of discrete possible choices.
Instead, in estimation problems, the unknown quantities are more of a numerical type.
They could even take continuous values.
And what we want to do is to come up with an estimate of an unknown quantity that is close to the true but unknown value of the quantity that we’re trying to estimate.
So here, our performance objective is in terms of some kind of distance function.
We want to be close to the truth.
And typically, we have a continuum of possible choices that is, our estimates can be general real numbers.
Generally speaking, these two types of problems, hypothesis testing and estimation, have some significant differences in the way that they are treated, as we will be seeing next.
