In this segment we start a new topic.
We will talk about the covariance of two random variables, which gives us useful information about the dependencies between these two random variables.
Let us motivate the concept by looking first at a special case.
Suppose that X and Y have zero means and that they there are discrete random variables.
If X and Y are independent, then the expectation of the product is the product of the expectations.
And since we have assumed zero means, this is going to be equal to zero.
But suppose instead that the joint PMF of X and Y is of the following kind.
Each point in this diagram is equally likely, so we have here a discrete uniform distribution on the discrete set which consists of the points shown in this diagram.
What we have in this particular example is that at most outcomes, positive values of X tend to go together with positive values of Y.
And negative values of X tend to go together with negative values of Y.
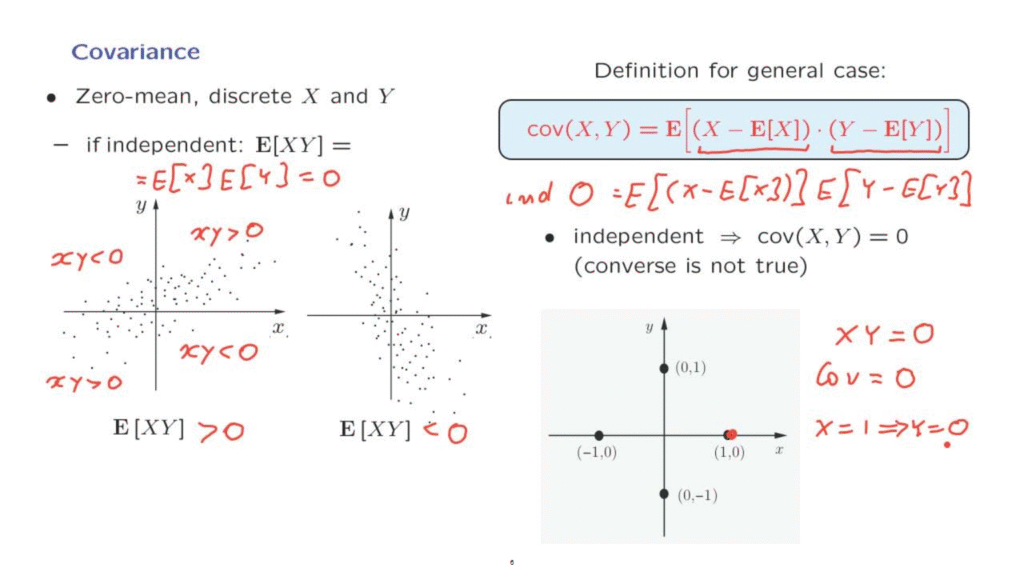
So most of the time we have outcomes in this quadrant, in which x times y is positive, or in this quadrant where x times y is, again, positive.
But some of the time we fall in this quadrant where x times y is negative, or in this quadrant where x times y is negative.
Since we have many more points here and here, on the average, the value of x times y is going to be positive.
On the other hand, if the diagram takes this form, then, most of the time, the pair x, y lies in this quadrant or in that quadrant where the product of x times y is negative.
So the random variables X and Y typically have opposite signs, and on the average, the expected value of X times Y is going to be negative.
So here we have a positive expectation, here we have a negative expectation of X times Y.
This quantity, the expected value of X times Y, tells us whether X and Y tend to move in the same or in opposite directions.

And this quantity is what we call the covariance, in the zero mean case.
Let us now generalize.
The random variables do not have to be discrete.
This quantity is well defined for any kind of random variables.
And if we have non-zero means, the covariance is defined by this expression.
What we have here is that we look at the deviation of X from its mean value, and the deviation of Y from its mean value, and we’re asking whether these two deviations tend to have the same sign or not, whether they move in the same direction or not.
If the covariance is positive, what it tells us is that whenever this quantity is positive so that X is above its mean, then, typically or usually, the deviation of Y from its mean will also tend to be positive.
To summarize, the covariance, in general, tells us whether two random variables tend to move together, both being high or both being low, in some average or typical sense.
Now, if the two random variables are independent, we already saw that in the zero mean case, this quantity– the covariance– is going to be 0.

How about the case where we have non-zero means?
Well, if we have independence, then we have the expected value of the product of two random variables.
X and Y are independent, so X minus the expected value, which is a constant, is going to be independent from Y minus its expected value.
And so, the covariance is going to be the product of two expectations.
But the expected value of X minus this constant is 0, and the same is true for this term as well.
So the covariance in this case is going to be equal to 0.
So in the independent case, we have zero covariances.
On the other hand, the converse is not true.
There are examples in which we have dependence but zero covariance.
Here is one example.
In this example there are four possible outcomes.
At any particular outcome, either X or Y is going to be 0.
So in this example the random variable X times Y is identically equal to 0.
The mean of X is also 0, the mean of Y is also 0 by symmetry, so the covariance is the expected value of this quantity.
And so the covariance, in this example, is equal to 0.
On the other hand, the two random variables, X and Y, are dependent.
If I tell you that X is equal to 1, then you know that this outcome has occurred.
And in that case, you are certain that Y is equal to 0.
So knowing the value of X tells you a lot about the value of Y and, therefore, we have dependence between these two random variables.