In this segment we introduce a simple but powerful tool, the basic counting principle, which we will be using over and over to deal with counting problems.
Let me describe the idea through a simple example.
You wake up in the morning and you find that you have in your closet 4 shirts, 3 ties, and 2 jackets.
In how many different ways can you get dressed today? To answer this question, let us think of the process of getting dressed as consisting of three steps, three stages.
You first choose a shirt, let’s say this one, and you have 4 choices of shirts.
But each shirt can be used together with 1 of the 3 available ties to make 3 different shirt-tie combinations.
But since we had 4 choices for the shirt, this means that we have 4 times 3, equals 12, shirt-tie combinations.
Finally, you choose a jacket.
Each shirt-tie combination can go together with either jacket, and so the fact that you have 2 jackets available doubles the number of options that you have, leading to 24 different options overall.
So 24 is the answer to this simple problem.
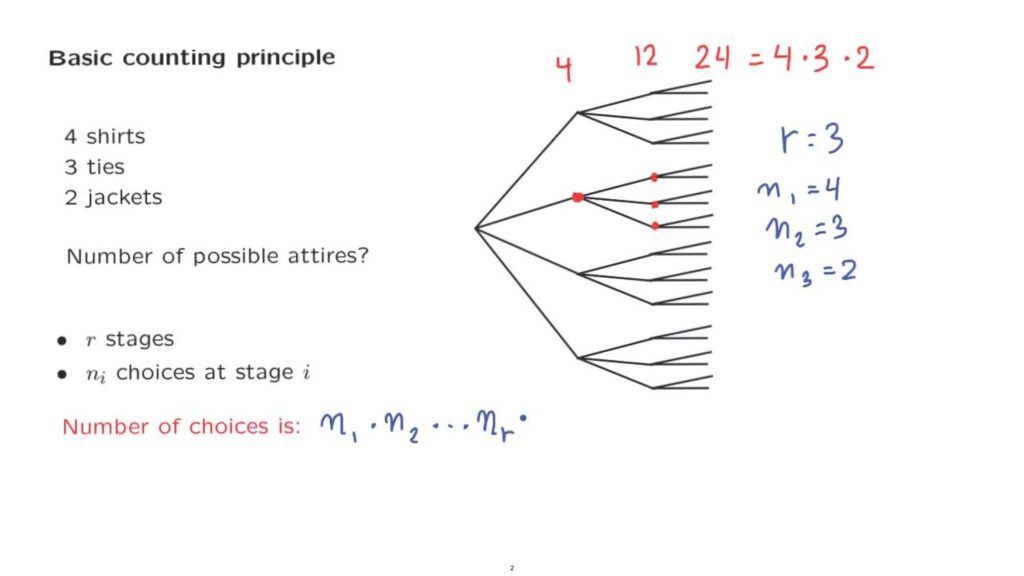
And how did the number 24 come about? Well, 24 is the same as the number of options you had in the first stage times the number of options you had in the second stage times the number of options you had in the third stage.
Let us generalize.
Suppose we want to construct some kind of object, and we’re going to construct it through a sequential process, through a sequence of r different stages.
In the example that we just considered, the number of stages was equal to 3.
At each one of the stages, you have a number of options that are available.
So in our example, at the first stage we had 4 options, at the second stage we had 3 options, and at the last stage we had 2 options.
What is important is that when you reach stage i, no matter what you chose, no matter what you did at the previous stages, the number of options that you will have available at stage i is going to be that fixed number, n-sub-i.
So what is the answer? How many different objects can you construct this way? Well, just generalizing from what we did in our specific example, the answer is the product of the number of choices or options that you had at each stage.
This is the counting principle.
It’s a very simple idea, but it is powerful.

It will allow us to solve fairly complicated counting problems.
However, before we go into more complicated problems, let us first deal with a few relatively easy examples.
In our first example, let us consider license plates that consist of 2 letters followed by 3 digits.
The question is, how many different license plates are there? We think of the process of constructing a license plate as a sequential process.
At the first stage we choose a letter, and we have 26 choices for the first letter.
Then we need to choose the second letter, and we have 26 choices for that one.
Then we choose the first digit.
We have 10 choices for it.
We choose the second digit, for which we have 10 choices.
And finally, we choose the last digit, for which we also have 10 choices.
So if you multiply these numbers, you can find the number of different license plates that you can make with 2 letters followed by 3 digits.
Now let us change the problem a little bit and require that no letter and no digit can be used more than once.
So, let us think of a process by which we could construct license plates of this kind.

In the first stage, we choose the first letter that goes to the license plate, and we have 26 choices.
Now, let us go into a second stage where we choose the second letter.
Because we used 1 letter in the first stage, this means that there’s only 25 available letters that can be used.
We only have 25 choices at the second stage.
Now, let us start dealing with the digits.
We choose the first digit, and we have 10 choices for it.
However, when we go and choose the next digit we will only have 9 choices, because 1 of the digits has already been used.
At this point, 2 digits have been used, which means that at the last stage we have only 8 digits to choose from.
So by multiplying these numbers, we can find out the answer to this question, the number of license plates if repetition is prohibited.
Let us now consider a different example.
Suppose that we start with a set that consists of n elements.
What we want to do is to take these n elements and order them.
A terminology that’s often used here is that we want to form a permutation of these n elements.
One way of visualizing permutations is to say that we’re going to take these elements of the set, which are unordered, and we’re going to place them in a sequence slots.
So we create n slots.
And we want to put each one of these elements into one of these slots.
How do we go about it? We think of putting the elements into slots, one slot at a time.
We first consider the first slot.
We pick one of the elements and put it there.
How many choices do we have at this stage? We have n choices, because we can pick any of the available elements and place it in that slot.
Next, we pick another element and put it inside the second slot.
How many choices do we have at this step? Well, we have already used one of the available elements, which means that there’s n minus 1 elements to choose from at the next stage.
At this point, we have used 2 of the elements.
There is n minus 2 that are left.
We pick one of them and put it in the third slot, and we have n minus 2 choices at this point.

We continue this way.
We keep going on.
At some point we have placed n minus 1 of the elements into slots.
There’s only one element left, and that element, necessarily, will get into the last slot.
There are no choices to be made at this point.
So the overall number of ways that we can carry out this process, put the elements into the n slots, by the counting principle is going to be the product of the number of choices that we had at each one of the stages.
So it’s the product of the numbers n, n minus 1, n minus 2, all the way down to 1.
And this product we denote as a shorthand this way, which we read as n factorial.
n factorial is the product of all integers from 1 all the way up to n.
And in particular, the number of permutations of n elements is equal to n factorial.
Let us now consider another example.
We start again with a general set, which consists of n elements.
And we’re interested in constructing a subset of that set.
In how many different ways can we do that? How many different subsets are there? Let us think of a sequential process through which we can choose the subset.
The sequential process proceeds by considering each one of the elements of our set, one at a time.
We first consider the first element, and here we have 2 choices.
Do we put it inside the set or not? So 2 choices for the first element.
Then we consider the second element.
Again, we have 2 choices.
Do we put it in the subset or not? We continue this way until we consider all the elements.
There’s n of them.

And the overall number of choices that we have is the product of 2 times 2 times 2, n times, which is 2 to the power n.
At this point, we can also do a sanity check to make sure that our answer is correct.
Let us consider the simple and special case where n is equal to 1, which means we’re starting with this set with 1 element, and we want to find the number of subsets that it has.
According to the answer that we derived, this should have 2 to the first, that is 2 subsets.
Which ones are they? One subset of this set is the set itself and the other subset is the empty set.
So we do have, indeed, 2 subsets out of that set, which agrees with the answer that we found.
Notice that when we count subsets of a given set, we count both the set itself, the whole set, and we also count the empty set.
All of these are subsets of our set.
At this point, we can now pause and you can try to answer some simple questions of the same kind as the ones that we just practiced.