A basketball coach has 20 players available.
Out of them, he needs to choose five for the starting lineup, and seven who would be sitting on the bench.
In how many ways can the coach choose these 5 plus 7 players? It is certainly a huge number, but what exactly is it? In this lecture, we will learn how to answer questions of this kind.
More abstractly, we will develop methods for counting the number of elements of a given set which is described in some implicit way.
Now, why do we care? The reason is that in many models, the calculation of probabilities reduces to counting.
Counting the number of elements of various sets.
Suppose that we have a probability model in which the sample space, Omega, is finite, and consists of n equally likely elements.
So each element has probability 1/n.
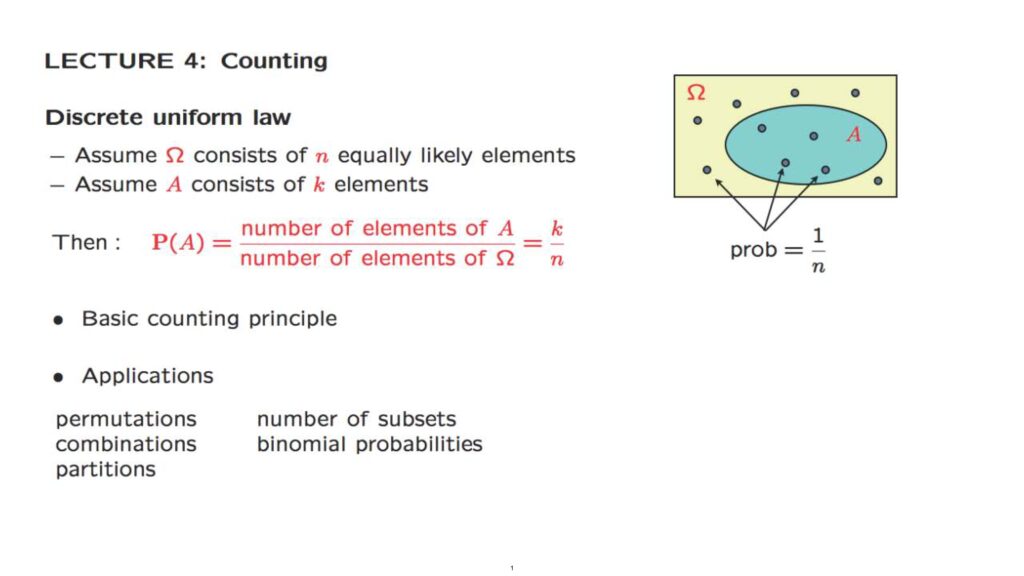
Suppose now that we’re interested in the probability of a certain set, A, which has k elements.
Since each one of the elements of A has probability 1/n, and since A has k distinct elements, then by the additivity axiom, the probability of A is equal to k times 1 over n.
Therefore to find the probability of A, all we have to do is to count the number of elements of Omega and the number of elements of A, and so determine the numbers k and n.
Of course, if a set is described explicitly through a list of its elements, then counting is trivial.
But when a set is given through some abstract description, as in our basketball team example, counting can be a challenge.
In this lecture, we will start with a powerful tool, the basic counting principle, which allows us to break a counting problem into a sequence of simpler counting problems.
We will then count permutations, subsets, combinations, and partitions.
We will see shortly what all of these terms mean.
In the process we will solve a number of example problems, and we will also derive the formula for the binomial probabilities, the probabilities that describe the number of heads in a sequence of independent coin tosses.
So, let us get started.