Independence is a very useful property.
Whenever it is true, we can break up complicated situations into simpler ones.
In particular, we can do separate calculations for each piece of a given model and then combine the results.
We’re going to look at an application of this idea into the analysis of reliability of a system that consists of independent units.
So we have a system that consists of a number, let’s say, n, of units.
And each one of the units can be “up” or “down”.
And it’s going to be “up” with a certain probability pi.
Furthermore, we will assume that unit failures are independent.
Intuitively, what we mean is that failure of some of the units does not the affect the probability that some of the other units will fail.
If we want to be more formal, we might proceed as follows.
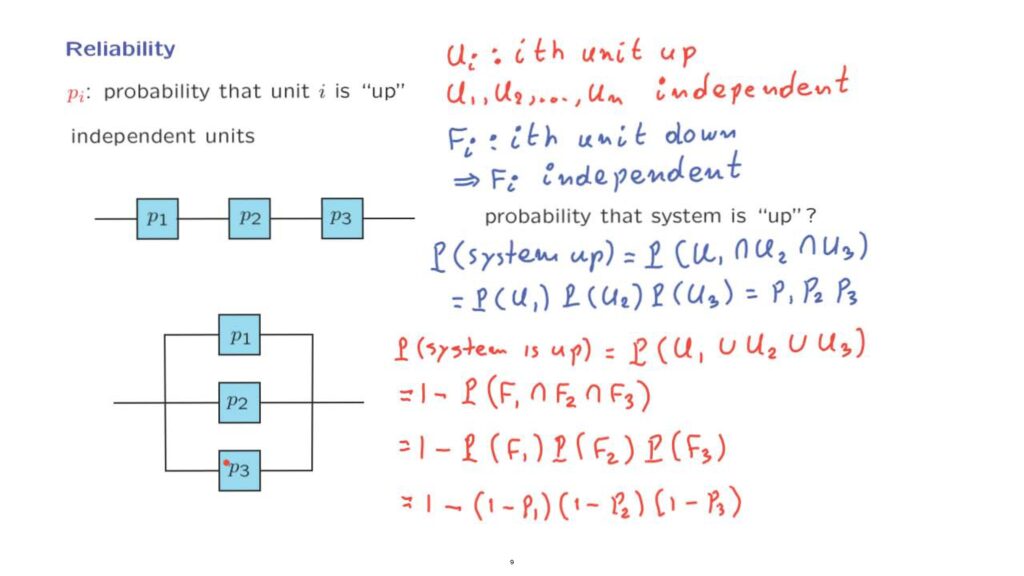
We could define an event Ui to be the event that the ith unit is “up”.
And then make the assumption that the events U1, U2, and so on up to Un, if we have n units, are independent.
Alternatively, we could define events Fi, where event Fi is the event that the ith unit is down, or that it has failed.
And we could assume that the events Fi are independent, but we do not really need a separate assumption.
As a consequence of the assumption that the Ui’s are independent, one can argue that the Fi’s are also independent.
How do we know that this is the case? If we were dealing with just two units, then this is a fact that we have already proved a little earlier.
We did prove that if two events are independent, then their complements are also independent.
Now that we’re dealing with multiple events here, a general number n, how do we argue? One approach would be to be formal and start from the definition of independence of the U events.
And that definition gives us a number of formulas.
Then manipulate those formulas to prove the conditions that are required in order to check that the events Fi are independent.
This is certainly possible, although it is a bit tedious.
However, the approach we will be taking in situations like this one is that we will use the intuitive understanding that we have of what independence means.
So independence in this context means that whether some units are “up” or down, does not change the probabilities that some of the other units will be “up” or down.
And by taking that interpretation, independence of the events that units are “up” is essentially the same as independence of the units [having] failed.

So we take this implication for granted and now we move to do some calculations for specific systems.
Consider a particular system that consists of three components.
And we will say that the system is “up”, if there exists a path from the left to the right that consists of units that are “up”.
So in this case, for the system to be “up”, we need all three components to be “up” and we proceed as follows.
The probability that the system is “up”– this is the event that the first unit is “up”, and the second unit is “up”, and the third unit is “up”.
And now we use independence to argue that this is equal to the probability that the first unit is “up” times the probability that the second unit is “up” times the probability that the third unit is “up”.
And in the notation that we have introduced this is just p1 times p2 times p3.
Now, let us consider a different system.
In this system, we will say that the system is “up”, again, if there exists a path from the left to the right that consists of units that are “up”.
In this particular case the system will be “up”, as long as at least one of those three components are “up”.
We would like again to calculate the probability that the system is “up”.
And the system will be “up”, as long as either unit 1 is “up”, or unit 2 is “up”, or unit 3 is “up”.
How do we continue from here? We cannot use independence readily, because independence refers to probabilities of intersections of events, whereas here we have a union.
How do we turn a union into an intersection? This is what De Morgan’s Laws allow us to do, and involves taking complements.

Instead of using formally De Morgan’s Laws, let’s just argue directly.
Let us look at this event.
That unit 1 fails, and unit 2 fails, and unit 3 fails.
What is the relation between this event and the event that we have here.
They’re complements.
Why is that? Either all units fail, which is this event, or there exists at least one unit, which is “up”.
So since this event is the complement of that event, this means that their probabilities must add to 1, and therefore we have this relation.
And now we’re in better shape, because we can use the independence of the events F to write this as 1 minus the product of the probabilities that each one of the units fails.
And with the notation that we have introduced using the pi’s, this is as follows.
The probability that unit 1 fails is 1 minus the probability that it is “up”.
Similarly, for the second unit, 1 minus the probability that it is “up”.
And the same for the third unit.
So we have derived a formula that tells us the reliability, the probability that a system of this kind is “up” in terms of the probabilities of its individual components.
You will have an opportunity to deal with more examples of this kind, a little more complicated, in the problem that follows.
And even more complicated, in one of the problem-solving videos that we will have available for you.