As an introduction to the main topic of this lecture sequence, let us go through a simple example and on the way, review what we have learned so far.
The example that we’re going to consider involves three tosses of a biased coin.
It’s a coin that results in heads with probability p.
We’re going to make this a little more precise.
And the coin is biased in the sense that this number p is not necessarily the same as one half.
We represent this particular probabilistic experiment in terms a tree that shows us the different stages of the experiment.
Each particular branch corresponds to a sequence of possible results in the different stages, and the leaves of this tree correspond to the possible outcomes.
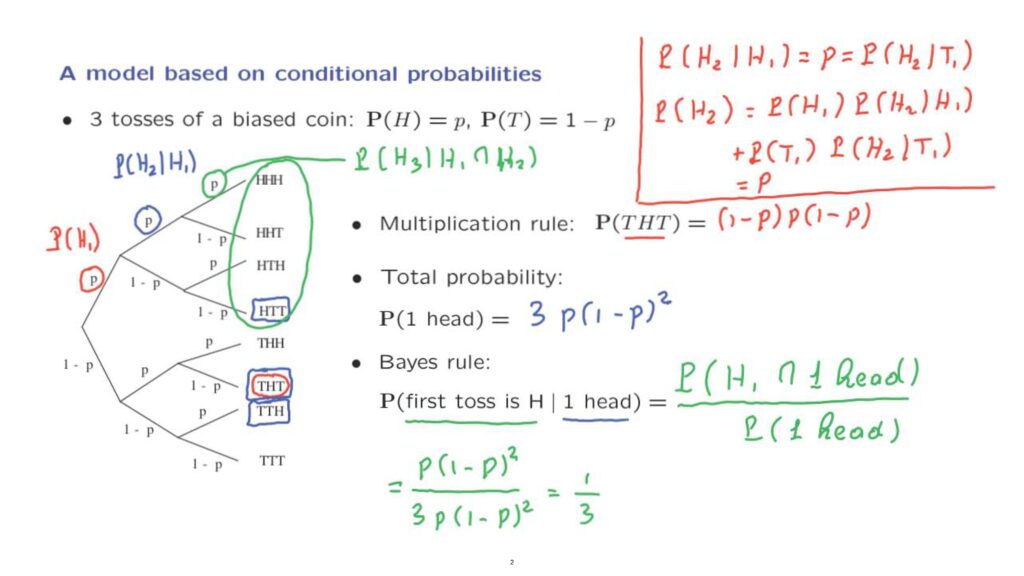
The branches of this tree are annotated by certain numbers, and these numbers are to be interpreted appropriately as probabilities or conditional probabilities.
So for example, this number here is interpreted as the probability of heads in the first toss, an event that we denote as H1.
This number here is to be interpreted as a conditional probability.
It’s the conditional probability of obtaining heads in the second toss given that the first toss resulted in heads.
And finally, this number here is to be interpreted as the conditional probability of heads in the third toss, given that the first toss resulted in heads and the second toss also resulted in heads.
Let us now continue with some calculations.
First, we’re going to practice the multiplication rule, which allows us to calculate the probability of a certain outcome.
In this case, the outcome of interest is tails followed by heads followed by tails.
So we’re talking about this particular outcome here.
According to the multiplication rule, to find the probability of a particular final outcome, we multiply probabilities and conditional probabilities along the path that leads to this particular outcome.
So in this case, it’s (1 minus p) times p times (1 minus p).
Let us now calculate the probability of a certain event.
The event of interest is the event that we obtain exactly one head in the three tosses.
This is an event that can happen in multiple ways.
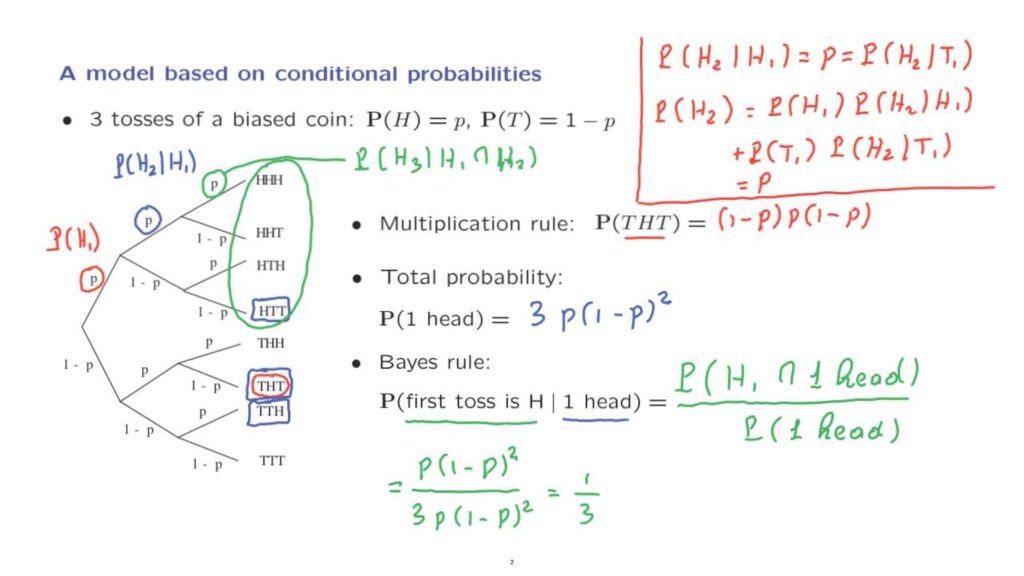
Here is one possibility where we have a single head.
Here’s another possibility.
And here’s a third one.
These are the three possible ways that we can have exactly one head, depending on where exactly that single head appears.
Is it in the first toss, in the second, or in the third.
To find the total probability of this event, we need to add the probability of the different outcomes that correspond to this event.
The probability of this outcome is p times (1 minus p) squared, the probability of this outcome is what we calculated.
It’s, again, p times (1 minus p) squared.
And the probability of the third one is also p times 1 minus p squared.
So the answer is 3p times (1 minus p) squared.
Notice that each one of the 3 different ways that this event can happen have the same probability.
So these 3 outcomes are equally likely.
Finally, let us calculate a conditional probability.
And this is essentially the Bayes rule.
Suppose that we were told that there was exactly one head.
So in particular, the blue event has occurred.
And we’re interested in the probability that the first toss is heads, which corresponds to this event here.
These are all the outcomes in which the first toss is equal to heads.
So given that the blue event happened, what is the probability that the green event happens? You can guess the answer, that it should be 1/3.

Why is that? Each one of these blue outcomes has the same probability.
So when you condition on the blue outcome having happened, the conditional probability of each one of these should be 1/3.
So given that the blue outcome happened, there’s probability 1/3 that this particular one has happened.
And this is the only one that makes the green event happen.
But let us see if we can derive this answer in a formal manner.
Let’s see if we’re going to get 1/3.
We use the definition of conditional probabilities.
The conditional probability is the ratio, first, of the probability that both events happen, divided by the probability of the conditioning event, which is the probability of 1 head.
Now, the probability of both events happening.
That we have exactly one head and the first toss is heads.
This is the intersection of the blue event and the green event which can happen only in this particular outcome, namely the sequence heads, tails, tails.
And has probability p times (1 minus p) squared.

The denominator is something that we have already calculated.
It’s 3p times (1 minus p) squared.
And so the final answer is 1/3 as we had guessed.
Let me now make a few comments about this particular example.
This particular example is pretty special in the following respect.
We have that of the probability of H2, heads in the second toss, given that the first one was heads, is equal to p.
And the same is true for the conditional probability of heads in the second toss given that the first one was tails.
In other words, our beliefs about what may happen in the second toss remain the same.
There’s a probability, p, of obtaining heads no matter what happened in the first toss.
Telling you the result of the first toss doesn’t change your beliefs about what may happen, and with what probability, in the second toss.
And if you were to calculate the unconditional probability of heads in the second toss, what you would get using the total probability theorem would be the following.
It’s probability of heads in the first toss times the probability of heads in the second, given heads in the first, plus the probability of tails in the first toss times the probability of heads in the second toss, given tails in the first.
And if you do the algebra, this turns out to be equal to p again.
So the unconditional probability of heads in the second toss turns out to be the same as the conditional probabilities.
Again, knowing what happened in the first toss doesn’t change your beliefs about the second toss, which were associated with this particular probability, p.
So what we’re going to do next is to generalize this special situation by giving a definition of independence of events, and then discuss various properties and concepts associated with independence.