Let us now conclude with a fun problem, which is also a little bit of a puzzle.
We are told that the king comes from a family of two children.
What is the probability that his sibling is female? Well, the problem is too loosely stated, so we need to start by making some assumptions.
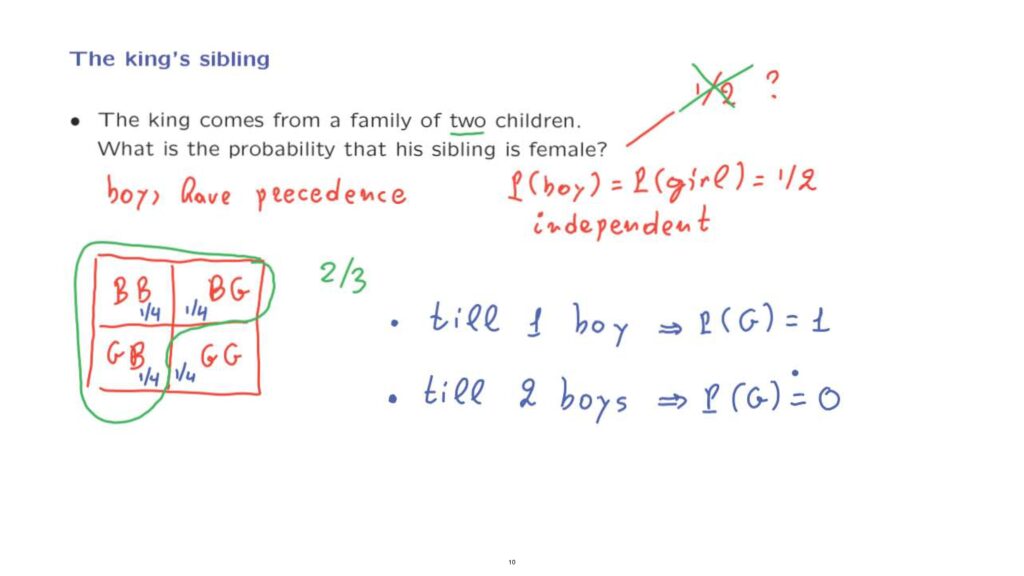
First, let’s assume that we’re dealing with an anachronistic kingdom where boys have precedence.
In other words, if the royal family has two children, one of which is a boy and one is a girl, it is always the boy who becomes king, even if the girl was born first.
Let us also assume that when a child is born, it has 50% probability of being a boy and 50% probability of being a girl.
And in addition, let’s assume that different children are independent as far as their gender is concerned.
Given these assumptions, perhaps we can argue as follows.
The king’s sibling is a child which is independent from the king.
Its gender is independent from the king’s gender, so it’s going to be a girl with probability 1/2.
And so this is one possible answer to this problem.
Is this a correct answer? Well, let’s see.
We have to make a more precise model, so let’s go ahead with it.
We have two children, so there are four possible outcomes– boy, boy; boy, girl; girl, boy; and girl, girl.
Each one of these outcomes has probability 1/4 according to our assumptions.
For example, the probability of a boy followed by a boy is 1/2 times 1/2, where we’re also using independence.
So each one of these four outcomes has the same probability, 1/4.
Now, we know that there is a king, so there must be at least one boy.
Given this information, one of the outcomes becomes impossible, namely the outcome girl, girl.
And we’re restricted to a smaller universe with only three possible outcomes.
Our new universe is this green universe, which includes all outcomes that have at least one boy, so that we can get a king.
We should, therefore, use the conditional probabilities that are appropriate to this new universe.
Since these three outcomes inside the green set have equal unconditional probabilities, they should also have equal conditional probabilities.
So each one of these three outcomes should have a conditional probability equal to 1/3.
In two of these outcomes the sibling is a girl and therefore, the conditional probability given that there is a king and therefore given that there is a boy, the conditional probability is going to be 2/3.
So this is actually the official answer to this problem, and this answer(1/2) is incorrect.
Are we satisfied with this answer? Maybe yes, maybe no.

Actually, some more assumptions are needed in order to say that 2/3 is the correct answer.
Let me state what these assumptions are.
We assume that the royal family decided to have exactly two children.
So the number two that we have here is not random.
It was something that was predetermined.
Once they decided to have the two children, they had them.
At least one turned out to be a boy and that boy became a king.
Under this situation, indeed, the probability that the sibling of the king is female is 2/3.
But these assumptions that I just stated are not the only possible ones.
Let’s consider some alternative assumptions.
For example, suppose that the royal family operated as follows.
They decided to have children until they get one boy.
What does this tell us? Well, since they had two children, this tells us something– that the first child was a girl.
So in this case, the probability that the king’s sibling is a girl is equal to 1.
The only reason why they had two children was because the first was a girl and then the second was a boy.
Suppose that the royal family made some different choices.
They decided to have children until they would get two boys, just to be sure that the line of succession was secured.
In this case, if we are told that there are only two children, this means that there were exactly two boys, because if one of the two children was a girl, the royal family would have continued.
So in this particular case, the probability that the sibling is a girl is equal to zero.
And you can think of other scenarios, as well, that might give you different answers.
So 2/3 is the official answer, as long as we make the precise assumptions that the number of children, the number two, was predetermined before anything else happened.
The general moral from this story is that when we deal with situations that are described in words somewhat vaguely, we must be very careful to state whatever assumptions are being made.
And that needs to be done before we are able to fix a particular probabilistic model.
This process of modeling will always be something of an art in which judgment calls will have to be made.