We end this lecture sequence by stepping back to discuss what probability theory really is and what exactly is the meaning of the word probability. In the most narrow view, probability theory is just a branch of mathematics.

We start with some axioms. We consider models that satisfy these axioms, and we establish some consequences, which are the theorems of this theory. You could do all that without ever asking the question of what the word “probability” really means.
Yet, one of the theorems of probability theory, that we will see later in this class, is that probabilities can be interpreted as frequencies, very loosely speaking. If I have a fair coin, and I toss it infinitely many times, then the fraction of heads that I will observe will be one half.
In this sense, the probability of an event, A, can be interpreted as the frequency with which event A will occur in an infinite number of repetitions of the experiment. But is this all there is?
If we’re dealing with coin tosses, it makes sense to think of probabilities as frequencies.
But consider a statement such as the “current president of my country will be reelected in the next election with probability 0.7”. It’s hard to think of this number, 0.7, as a frequency. It does not make sense to think of infinitely many repetitions of the next election.
In cases like this, and in many others, it is better to think of probabilities as just some way of describing our beliefs.
And if you’re a betting person, probabilities can be thought of as some numerical guidance into what kinds of bets you might be willing to make. But now if we think of probabilities as beliefs, you can run into the argument that, well, beliefs are subjective.
Isn’t probability theory supposed to be an objective part of math and science? Is probability theory just an exercise in subjectivity? Well, not quite. There’s more to it.
Probability, at the minimum, gives us some rules for thinking systematically about uncertain situations. And if it happens that our probability model, our subjective beliefs, have some relation with the real world, then probability theory can be a very useful tool for making predictions and decisions that apply to the real world.
Now, whether your predictions and decisions will be any good will depend on whether you have chosen a good model. Have you chosen a model that’s provides a good enough representation of the real world?
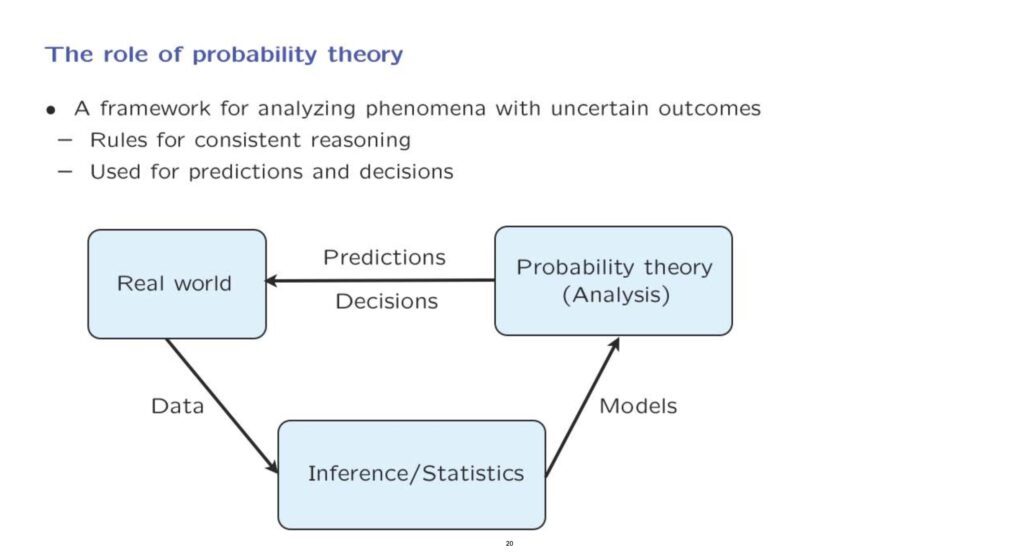
How do you make sure that this is the case? There’s a whole field, the field of statistics, whose purpose is to complement probability theory by using data to come up with good models. And so we have the following diagram that summarizes the relation between the real world, statistics, and probability.
The real world generates data. The field of statistics and inference uses these data to come up with probabilistic models.
Once we have a probabilistic model, we use probability theory and the analysis tools that it provides to us. And the results that we get from this analysis lead to predictions and decisions about the real world.