We now revisit the exponential random variable that we introduced earlier and develop some intuition about what it represents.
We do this by establishing a memorylessness property, similar to the one that we established earlier in the discrete case for the geometric PMF.
Suppose that it is known that light bulbs have a lifetime until they burn out, which is an exponential random variable.
You go to a store, and you are given two choices, to buy a new light bulb, or to buy a used light bulb that has been working for some time and has not yet burned out.
Which one should you take? We want to approach this question mathematically.
So let us denote by capital T the lifetime of the bulb.

So time starts at time 0, and then at some random time that we denote by capital T, the light bulb will burn out.
And we assume that this random variable is exponential with some given parameter lambda.
In one of our earlier calculations, we have shown that the probability that capital T is larger than some value little x falls exponentially with that value x.
We are now told that a certain light bulb has already been operating for t time units without failing.
So we know that the value of the random variable capital T is larger than little t.
We are interested in how much longer the light bulb will be operating, and so we look at capital X, which is the remaining lifetime from the current time until the light bulb burns out.
So capital X is this particular random variable here, and it is equal to capital T minus little t.
Let us now calculate the probability that the light bulb lasts for another little x time units.
That is, that this random variable, capital X, is at least as large as some little x.
That is, that the light bulb remains alive until time t plus x.
We use the definition of conditional probabilities to write this expression as the probability that capital X is bigger than little x.
On the other hand, capital X is T minus t, so we write it this way– T minus t is bigger than little x, and also that T is bigger than little t, divided by the probability of the conditioning event.
Just write this event in a cleaner form, capital T being larger than little t plus x and being larger than little t, again divided by the probability of the conditioning event.

And now notice that capital T will be greater than little t and also greater than little t plus x, that is, capital T is larger than this number and this number, if and only if it is larger than this second number here.
So in other words, the intersection of these two events is just this event here, that capital T is larger than little t plus x.
Now, we can use the formula for the probability that capital T is larger than something.
We apply this formula, except that instead of little x, we have t plus x.
And so here we have e to the minus lambda t plus x divided by the probability that capital T is bigger than t.
So we use this formula, but with little t in the place of little x, and we obtain e to the minus lambda t.
We have a cancellation, and we’re left with e to the minus lambda x, which is a final answer in this calculation.
What do we observe here? The probability that the used light bulb will live for another x time units is exactly the same as the corresponding probability that the new light bulb will be alive for another x time units.
So new and used light bulbs are described by the same probabilities, and they’re probabilistically identical, the same.
Differently said, the used light bulb does not remember, and it is not affected by how long it has been running.
And this is the memorylessness property of exponential random variables.
Let us now build some additional insights on exponential random variables.
We have a formula for the density, the PDF.
And from this, we can calculate the probability that T lies in a small interval.
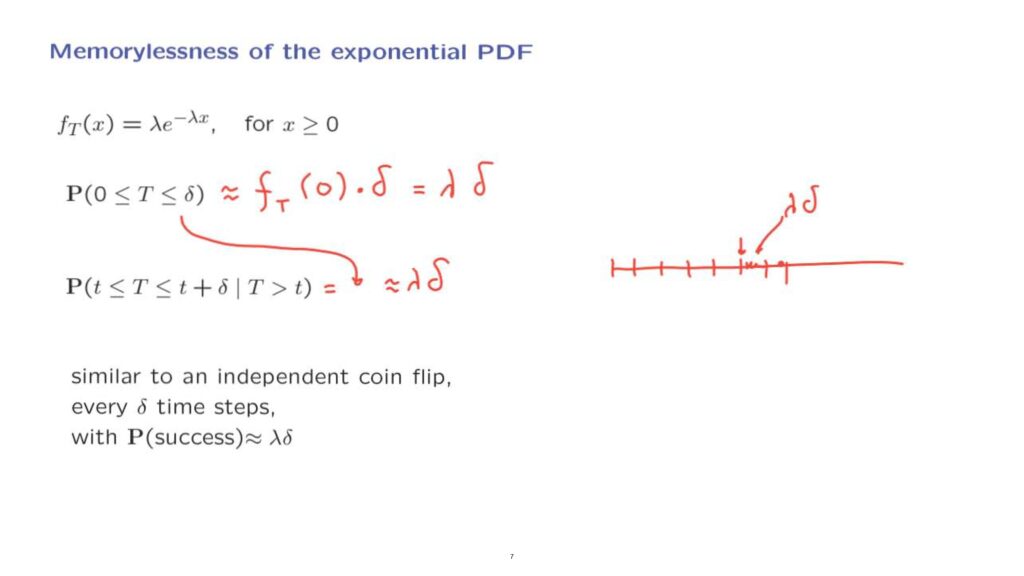
For example, for a small delta, this probability here is going to be approximately equal to the density of T evaluated at 0 times delta, which is lambda times e to the 0, which is 1, times delta.
What if we are told that the light bulb has been alive for t time units? What is the probability that it burns out during the next delta times units? Since a used but still alive light bulb is probabilistically identical to a new one, this conditional probability is the same as this probability here that a new light bulb burns out in the next delta times units.
And so this is also approximately equal to lambda delta.
So we see that independently of how long a light bulb has been alive, during the next delta time units it will have a lambda delta probability of failing.
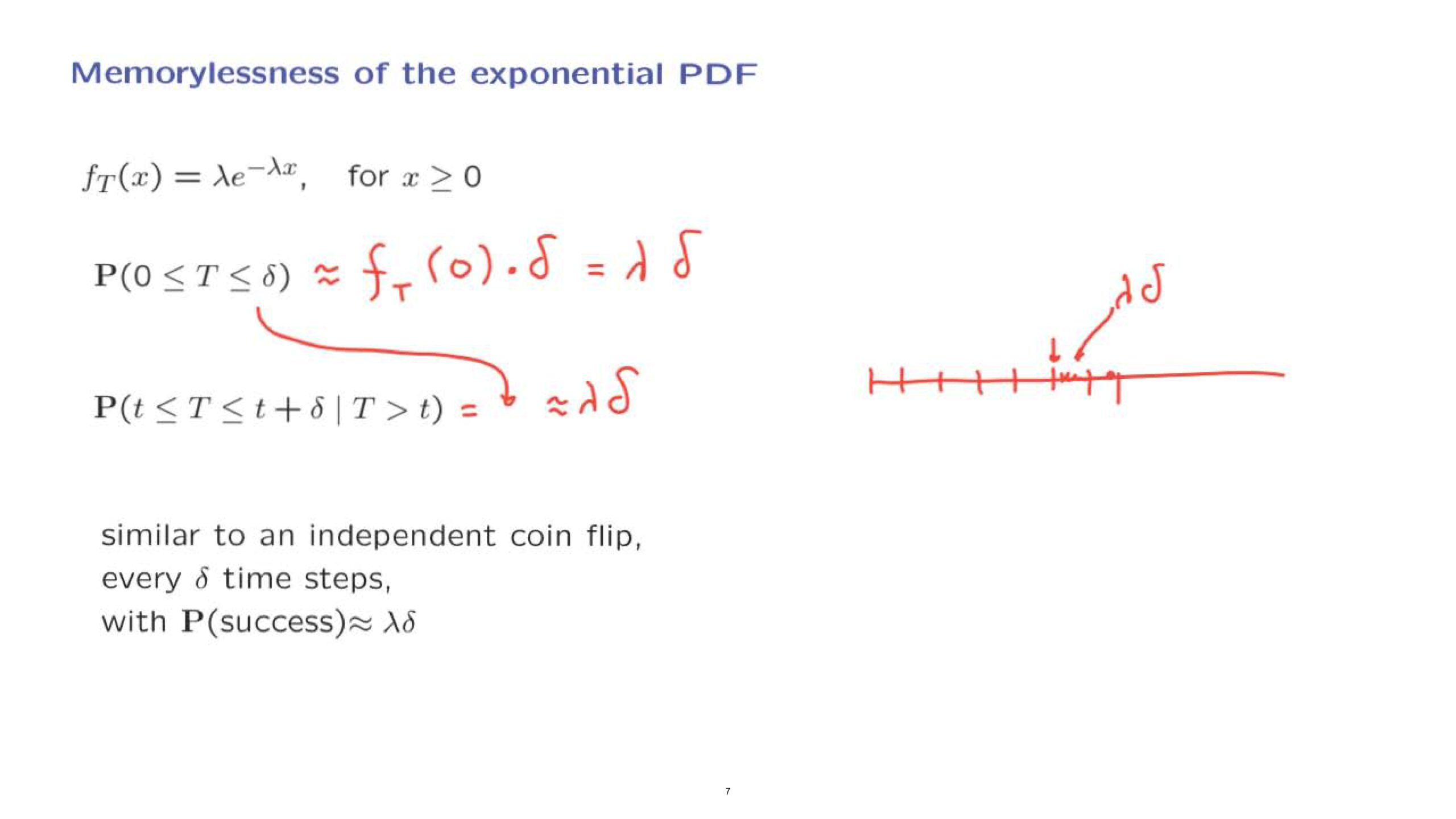
One way of thinking about this situation is that the time interval is split into little intervals of length delta.
And as long as the light bulb is alive, if it is alive at this point, it will have probability lambda delta of burning out during the next interval of length delta.
This is like flipping a coin.
Once every delta time steps, there is a probability lambda delta that there is a success in that coin flip, where success corresponds to having the light bulb actually burn down, and the exponential random variable corresponds to the total time elapsed until the first success.
In this sense, the exponential random variable is a close analog of the geometric random variable, which was the time until the first success in a discrete time setting.
This analogy turns out to be the foundation behind the Poisson process that we will be studying later in this course.