Let us now look at an example.
Consider a piecewise constant PDF of the form shown in this diagram.
Suppose that we condition on the event that x lies between a plus b over 2, which is here, and b.
So we’re conditioning on x lying in this particular red interval.
What is the conditional PDF? The conditional PDF is going to be 0 outside of the interval on which we are conditioning.
So the conditional PDF is 0 in this range, and also, it is 0 in this range.
Within the range of values of x that are allowed given the conditioning information, the conditional PDF must retain the same shape as the unconditional one.
And the unconditional one is constant in that range.
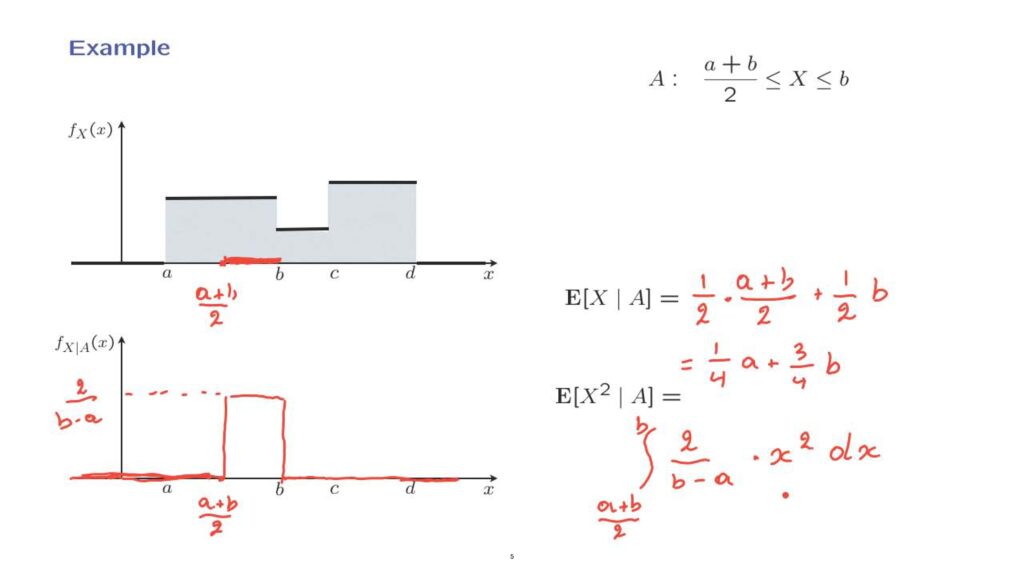
So the conditional PDF will also be a constant.
Because in this case the length of this interval is half of the distance between b minus a– so the length of this interval is b minus a over 2– in order for the area under this curve to be equal to 1, it means that the height of this curve has to be equal to 2 over b minus a.
The conditional expectation in this example is just the ordinary expectation but applied to the conditional model.
Since the conditional PDF is uniform, the conditional expectation will be the midpoint of the range of this conditional PDF.
And in this case, the midpoint is 1/2 the left end of the interval, which is a plus b over 2 plus 1/2 the right end point of the interval, which is b.
And so this evaluates to 1/4 times a plus 3/4 times b.
We can also calculate the expected value of X squared in the conditional model using the expected value rule.
According to the expected value rule, it’s going to be an integral of the conditional PDF, which is 2 over b minus a multiplied by x squared.
And this integral runs over the range where the conditional PDF is actually non-zero.
So it’s an integral that ranges from a plus b over 2 up to b.
And this an integral which is not too hard to evaluate, and there’s no point in carrying out the evaluation to the end.