Let us now give an example of a continuous random variable– the uniform random variable.
It is patterned after the discrete random variable.
Similar to the discrete case, we will have a range of possible values.
In the discrete case, these values would be the integers between a and b.
In the continuous case, any real number between a and b will be possible.
In the discrete case, these values were equally likely.
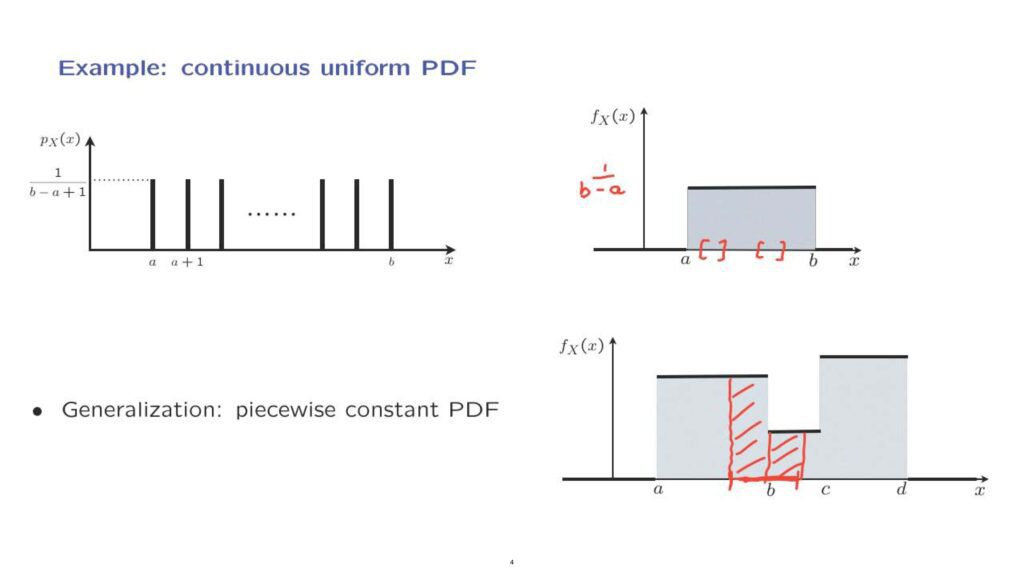
In the continuous case, at all points, we have the same height for the probability density function.
And as a consequence, if we take two intervals that have the same length, then these two intervals will be assigned the same probability.
Intuitively, uniform random variables model the following situation.
We know that the numerical value of the random variable will be between a and b.
But we know nothing more.
We have no reason to believe that certain locations are more likely than others.
And in this sense, the uniform random variable models a situation of complete ignorance.
By the way, since probabilities must add to 1, the area of this rectangle must be equal to 1.
And therefore, the height of this rectangle has to be 1 over b minus a, so that we have a height of 1 over b minus a.
We have a length of b minus a.

So the product of the two, which is the area, is equal to 1.
Finally, here’s a more general PDF, which is piecewise constant.
One thing to notice is that this, in particular, tells us that PDFs do not have to be continuous functions.
They can have discontinuities.
Of course, for this to be a legitimate PDF, the total area under the curve, which is the sum of the areas of the rectangles that we have here, must be equal to 1.
With a piecewise constant PDF, we can calculate probabilities of events fairly easy.
For example, if you wish to find the probability of this particular interval, which is going to be the area under the curve, that area really consists of two pieces.
We find the areas of these two rectangles, add them up, and this gives us the total probability of this particular interval.
So at this point, our agenda, moving forward, will be twofold.
First, we will introduce some interesting continuous random variables.
We just started with the presentation of the uniform random variable.
And then, we will also go over all of the concepts and results that we have developed for discrete random variables and develop them again for their continuous counterparts.