We now come to our last major class of counting problems.
We will count the number of ways that a given set can be partitioned into pieces of given sizes.
We start with a set that consists of n different elements.
And we have r persons.
We want to give n1 items to the first person, give n2 items to the second person, and so on.
And finally, we want to give n-sub-r items to the rth person.
These numbers, n1, n2, up to nr are given to us, how many items each person should get.
And these numbers must add to n so that every item in the original set is given to some person.
We want to count to the number of ways that this can be done.
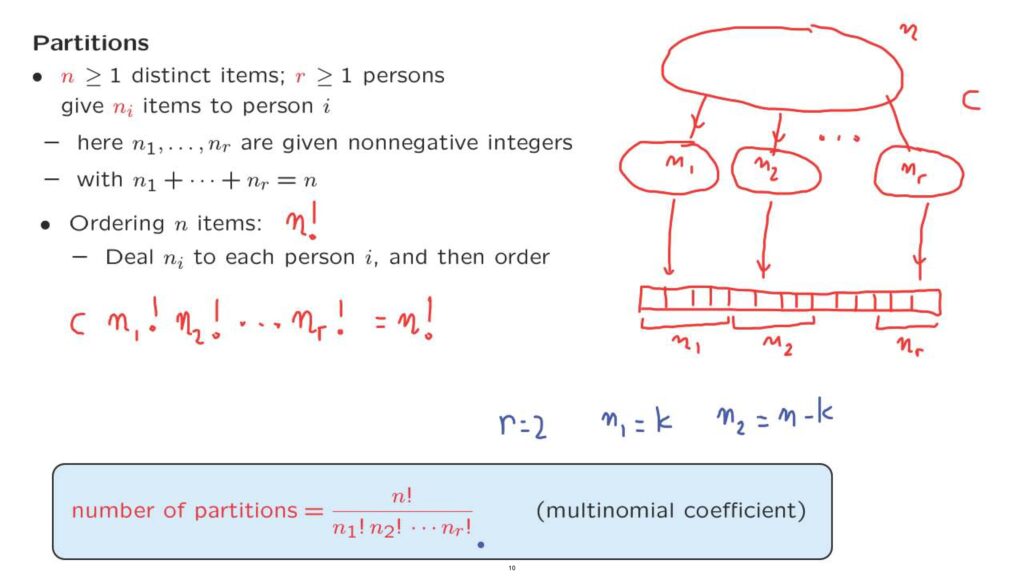
This is the number of ways that we can partition a given set into subsets of prescribed sizes.
Let’s use c to denote the number of ways this can be done.
We want to calculate this number c.
Instead of calculating directly, we’re going to use the same trick that we employed when we counted combinations and derived the binomial coefficient.
That is, we’re going to consider, in a much simpler counting problem, the problem of ordering n items, taking the n items in our original set and putting them in an ordered list.
Of course, we know in how many ways this can be done.
Ordering n items can be done in n factorial ways.
This is the count of the number of permutations of n items.
But now let us think of a different way of ordering the n items, an indirect way.
It proceeds according to the following stages.
We start with the n items.
And we first distribute them to the different persons.
Having done that, then we ask person one to take their items, order them, and put them in the first n1 slots of our list.
Then person two takes their items and puts them into the next n2 slots in our list.
We continue this way.
And finally, the last person takes the items that they possess and puts them in the last n-sub-r slots in this list.

In how many ways can this process be carried out? We have c choices on how to partition the given set into subsets.
Then person one has n1 factorial choices on how to order the n1 items that that person processes.
Person two has n2 factorial choices for how to order the n2 items that it possesses, and so on until the last person, who has nr factorial choices for ordering their elements.
This multi-stage process results in an ordered list of the n terms.
This is the number of ways these multi-stage process can be carried out.
On the other hand, we know that the number of possible orderings of the items is n factorial.
So we have this equality.
We can solve this for c.
And we find the answer, that the number of ways that the n items can be partitioned into subsets of the given sizes is n factorial divided by the product of the factorials of the different ni’s.
This particular expression is called the multinomial coefficient, and it generalizes the binomial coefficient.
The binomial coefficient was referring to the case where we essentially split our set into one subset with k elements, and then the second subset gets the remaining elements.
So the special case where r is equal to 2, and n1 is equal to k, n2 equals to n minus k, this corresponds to a partition of a set into two subsets, or what is the same just selecting the first subset and putting everything else in the second subset.
And you can check that in this particular case, the expression for the multinomial coefficient agrees with the expression that we had derived for the binomial coefficient.