Let us now study a very important counting problem, the problem of counting combinations.
What is a combination? We start with a set of n elements.
And we’re also given a non-negative integer, k.
And we want to construct or to choose a subset of the original set that has exactly k elements.
In different language, we want to pick a combination of k elements of the original set.
In how many ways can this be done? Let us introduce some notation.
We use this notation here, which we read as “n-choose-k,” to denote exactly the quantity that we want to calculate, namely the number of subsets of a given n-element set, where we only count those subsets that have exactly k elements.
How are we going to calculate this quantity? Instead of proceeding directly, we’re going to consider a somewhat different counting problem which we’re going to approach in two different ways, get two different answers, compare those answers, and by comparing them, we’re going to get an equation, which is going to give us in the end, the desired number.

The alternative problem that we’re going to use is the following.
We start, as before, with our given set that consists of n elements.
But instead of picking a subset, what we want to do is to construct a list, an ordered sequence, that consists of k distinct elements taken out of the original set.
So we think of having k different slots, and we want to fill each one of those slots with one of the elements of the original set.
In how many ways can this be done? Well, we want to use the counting principle.
So we want to decompose this problem into stages.
So what we can do is to choose each one of the k items that go into this list one at a time.
We first choose an item that goes to the first position, to the first slot.

Having used one of the items in that set, we’re left with n minus 1 choices for the item that can go into the second slot.
And we continue similarly.
When we’re ready to fill the last slot, we have already used k minus one of the items, which means that the number of choices that we’re going to have at that stage is n minus k plus 1.
At this point, it’s also useful to simplify that expression a bit.
We observe that this is the same as n factorial divided by n the minus k factorial.
Why is this the case? You can verify that this is correct by moving the denominator to the other side.
And when you do that, you realize that you have the product of all terms from n down to n minus k plus 1.
And then you have the product of n minus k going all the way down to one.
And that’s exactly the product, which is the same as n factorial.

It’s a product of all integers from n all the way down to 1.
So this was the first method of constructing the list that we wanted.
How about a second method? What we can do is to first choose k items out of the original set, and then take those k terms and order them in a sequence to obtain an ordered list.
So we construct our ordered list in two stages.
In the first stage, how many choices [do] we have? That’s the number of subsets with k elements out of the original set.
This number, we don’t know what it is.
That’s what we’re trying to calculate.
But we have a symbol for it.
It’s n-choose-k.
How about the second stage? We have k elements, and we want to arrange them in a sequence.
That is, we want to form a permutation of those k elements.
This is a problem that we have already studied, and we know that the answer is k factorial.
According to the counting principle, the number of ways that this two-stage construction can be made is equal to the product of the number of ways, number of options that we have in the first stage times the number of options that we have in the second stage.

So this is one answer for the number of possible ordered sequences.
This is another answer.
Of course, both of them are correct.
And therefore, they have to be equal.
And by using that equality, we can now find a formula for this coefficient n-choose-k simply by taking this k factorial factor and sending it to the denominator of that expression.
So by equating this expression with that expression here, we find the final answer, which is that the number of choices, n-choose-k, is equal to this expression here.
Now, this expression is valid only for numbers that make sense.
So n can be any integer, any non-negative integer.
And k, the only k’s that make sense, would be k’s from 0, 1 up to n.
You may be wondering about some of the extreme cases of that formula.
What does it mean for n to be 0 or for k equal to 0? So let us consider now some of these extreme cases and make a sanity check about this formula.
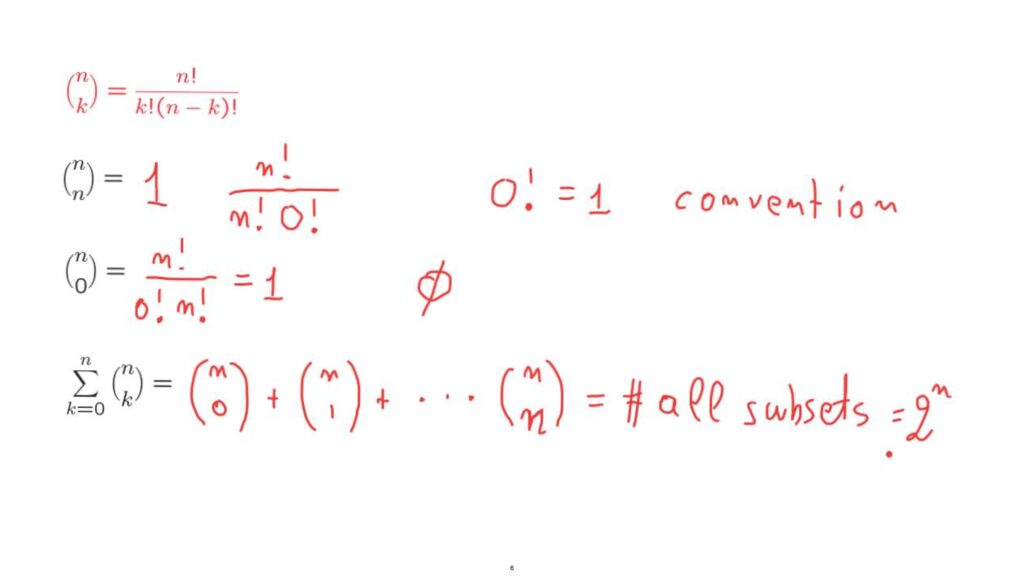
So this is the formula that we have and that we want to check.
The first case to consider is the extreme case of n-choose-n.
What does that correspond to? Out of a set with n elements, we want to choose a subset that has n elements.
There’s not much of a choice here.
We just have to take all of the elements of the original set and put them in the subset.
So the subset is the same as the set itself.
So we only have one choice here.
That should be the answer.
Let’s check it with the formula.
The formula gives us n factorial divided by n factorial.
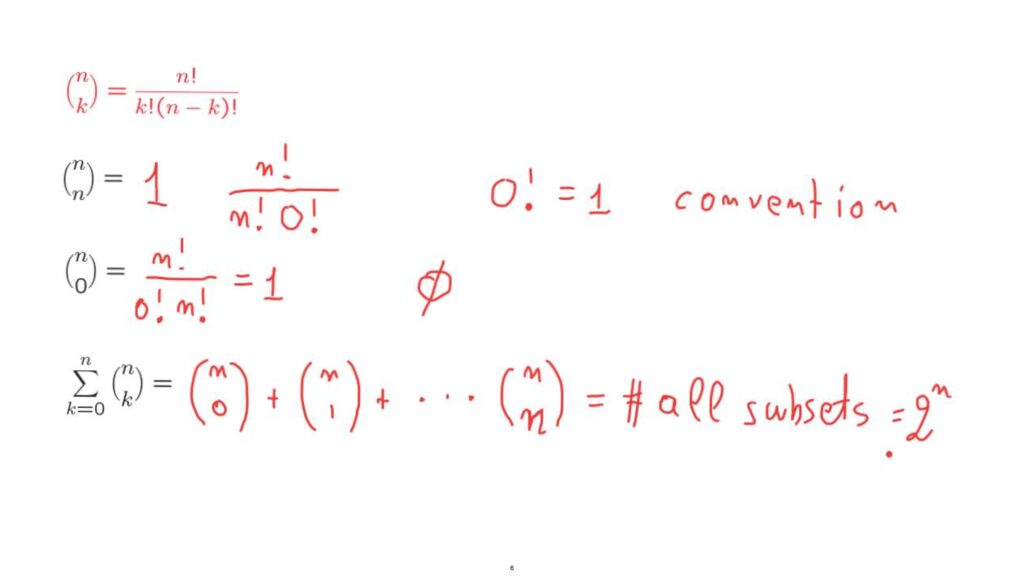
And then, since k is equal to n, here we get zero factorial.
Is this correct? Well, it becomes correct as long as we adopt the convention that zero factorial is equal to 1.
We’re going to adopt this convention and keep it throughout this course.
Let’s look at another extreme case now, the coefficient n choose 0.
This time let us start from the formula.
The formula tells us that this should be n factorial divided by 0 factorial and divided by n factorial, since the number k is equal to 0.
Using the convention that we have, this is equal to 1.
So this is, again, equal to 1.
Is it the correct answer?
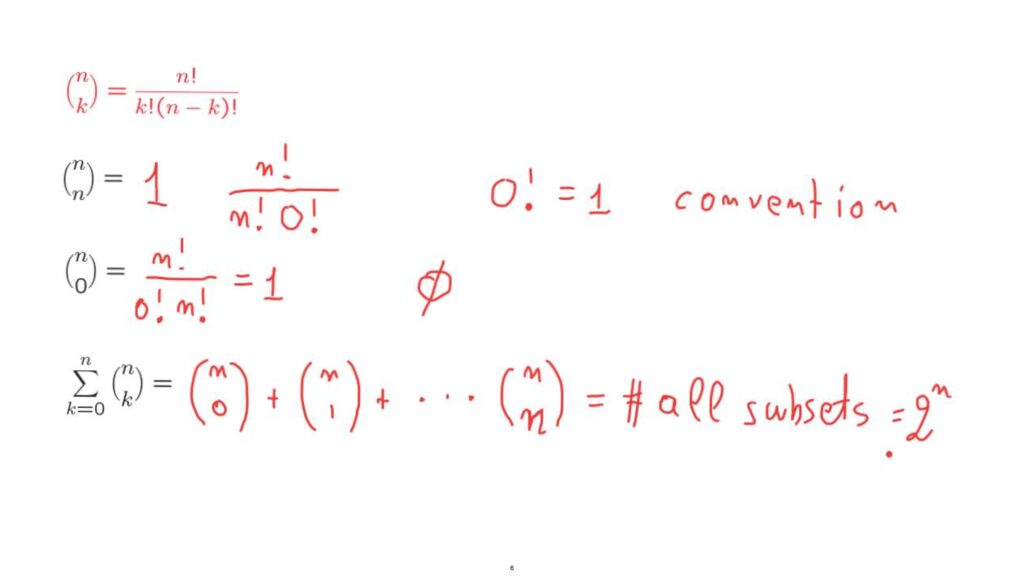
How many subsets of a given set are there that have exactly zero elements? Well, there’s only one subset that has exactly 0 elements, and this is the empty set.
So this explains this particular answer and shows that it is meaningful and that it makes sense.
Now, let us use our understanding of those coefficients to solve a somewhat harder problem.
Suppose that for some reason, you want to calculate this sum.
What is it going to be? One way of approaching this problem is to use the formula for these coefficients, do a lot of algebra.
And if you’re really patient and careful, eventually you should be able to get the right answer.
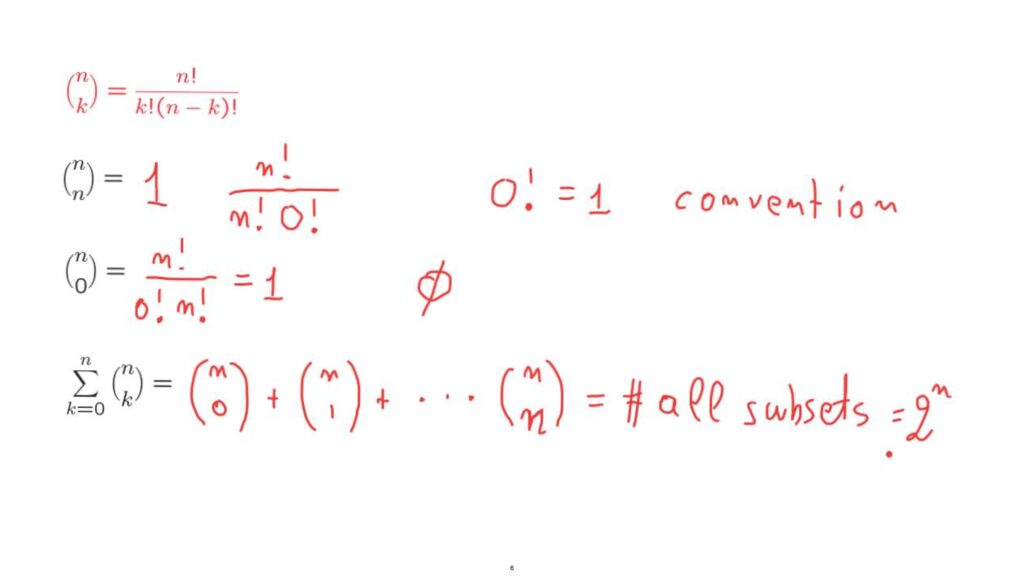
But this is very painful.
Let us think whether there’s a clever way, a shortcut, of obtaining this answer.
Let us try to think what this sum is all about.
This sum includes this term, which is the number of zero-element subsets.
This number, which is the number of subsets that have one element.
And we keep going all the way to the number of subsets that have exactly n elements.
So we’re counting zero-element subsets, one-element subsets, all the way up to n.
So what we’re counting really is the number of all subsets of our given set.
But this is a number that we know what it is.
The number of subsets of a given set with n elements is 2 to the n.
So by thinking carefully and interpreting the terms in this sum, we were able to solve this problem very fast, something that would be extremely tedious if we had tried to do it algebraically.
For some practice with this idea, why don’t you pause at this point and try to solve a problem of a similar nature?