As promised, we will now start developing generalizations of the different calculations that we carried out in the context of the radar example.
The first kind of calculation that we carried out goes under the name of the multiplication rule.
And it goes as follows.
Our starting point is the definition of conditional probabilities.
The conditional probability of A given another event, B, is the probability that both events have occurred divided by the probability of the conditioning event.
We now take the denominator term and send it to the other side of this equality to obtain this relation, which we can interpret as follows.
The probability that two events occur is equal to the probability that a first event occurs, event B in this case, times the conditional probability that the second event, event A, occurs, given that event B has occurred.
Now, out of the two events, A and B, we’re of course free to choose which one we call the first event and which one we call the second event.
So the probability of the two events happening is also equal to an expression of this form, the probability that A occurs times the conditional probability that B occurs, given that A has occurred.
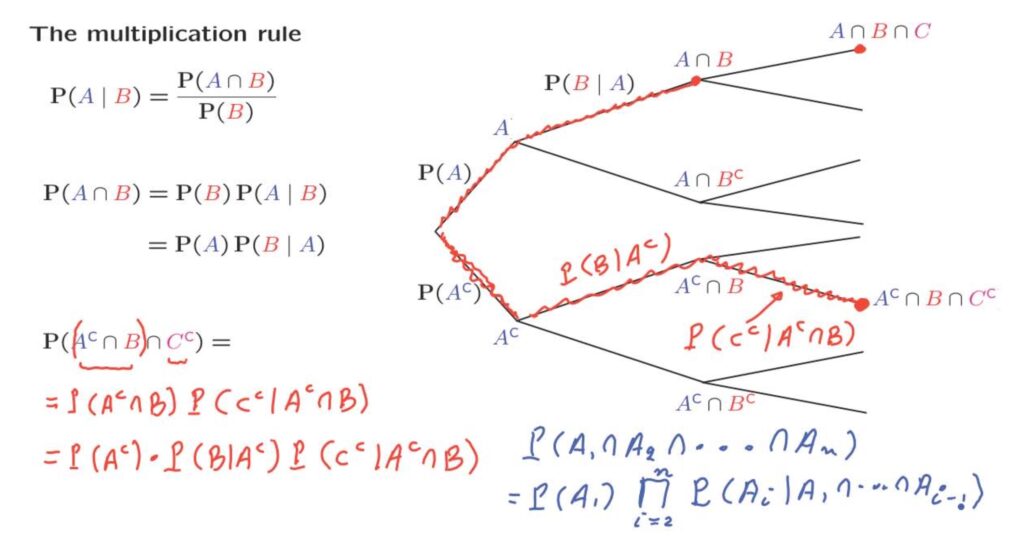
We used this formula in the context of a tree diagram.
And we used it to calculate the probability of a leaf of this tree by multiplying the probability of taking this branch, the probability that A occurs, times the conditional probability of taking this branch, the probability that event B also occurs given that event A has occurred.
How do we generalize this calculation? Consider a situation in which the experiment has an additional third stage that has to do with another event, C, that may or may not occur.

For example, if we have arrived here, A and B have both occurred.
And then C also occurs, then we reach this particular leaf of the tree.
Or there could be other scenarios.
For example, it could be the case that A did not occur.
Then event B occurred, and finally, event C did not occur, in which case we end up at this particular leaf.
What is the probability of this scenario happening? Let us try to do a calculation similar to the one that we used for the case of two events.
However, we need to deal here with three events.
What should we do? Well, we look at the intersection of these three events and think of it as the intersection of a composite event, A complement intersection B, then intersected with the event C complement.
Clearly, you can form the intersection of three events by first taking the intersection of two of them and then intersecting with a third.
After we group things this way, we’re dealing with the probability of two events happening, this composite event and this ordinary event.
And the probability of two events happening is equal to the probability that the first event happens, and then the probability that the second event happens, given that the first one has happened.
Can we simplify this even further? Yes.
The first term is the probability of two events happening.
So it can be simplified further as the probability that A complement occurs times the conditional probability that B occurs, given that A complement has occurred.
And then we carry over the last term exactly the way it is.
The conclusion is that we can calculate the probability of this leaf by multiplying the probability of the first branch times the conditional probability of the second branch, given that the first branch was taken, and then finally multiply with the probability of the third branch, which is the probability that C complement occurs, given that A complement and B have already occurred.
In other words, we can calculate the probability of a leaf by just multiplying the probabilities of the different branches involved and where we use conditional probabilities for the intermediate branches.

At this point, you can use your imagination to see that such a formula should also be valid for the case of more than three events.
The probability that a bunch of events all occur should be the probability of the first event times a number of factors, each corresponding to a branch in a tree of this kind.
In particular, the probability that events A1, A2, up to An all occur is going to be the probability that the first event occurs times a product of conditional probabilities that the i-th event occurs, given that all of the previous events have already occurred.
And we obtain a term of this kind for every event, Ai, after the first one, so this product ranges from 2 up to n.
And this is the most general version of the multiplication rule and allows you to calculate the probability of several events happening by multiplying probabilities and conditional probabilities.